数据校验码
数据在存取和传送过程中可能会发生错误,数据校验码是指那些能够发现错误或能够自动纠正错误的数据编码,又称为检错纠错码。任意两个码字之间变化所需改变的最少位数称为数据校验码的码距,如:8421码的0000与0001转换仅需变动一位,故码距为1,码距为1的编码没有检错能力。码距越大,检错纠错能力越强,且检错能力总是大于等于纠错能力。
具有检错纠错能力的原理:在编码中,除去合法的码字外,再加进一些非法的码字,当某个码字出错时就会变为非法码字。合理安排非法码字数量和编码规则即可达到纠错目的。
1.奇偶校验码
最简单的数据校验码,码距为2。可以检测一位(或奇数个位)错误,但无法确定出错位置。这种方式检错能力低,但是应用最广泛,常用于存储器读写检查或ASCII字符传送检查。
实现方法:奇(偶)校验即校验位的取值使整个校验码中1的个数为奇(偶)数,校验位为新增一位作为最高位。通常采用奇校验,奇校验不会出现全0码,便于判别。奇校验结果取反即偶校验结果。
| 有效信息(8位) | 奇校验码(9位) | 偶校验码(9位) |
|---|---|---|
| 0000,0000 | 1,0000,0000 | 0,0000,0000 |
| 0101,0100 | 0,0101,0100 | 1,0101,0100 |
| 0111,1111 | 0,0111,1111 | 1,0111,1111 |
| 1111,1111 | 1,1111,1111 | 0,1111,1111 |
校验检测:在生成校验位之后,将9个数(8位信息位和1位奇偶校验位)送入检测电路,若读出代码无错,则“校验出错”输出0,否则输出1。 \(S_{偶校验出错}=P_校 \bigoplus D_1 \bigoplus D_2 \bigoplus D_3 \bigoplus D_4 \bigoplus D_5 \bigoplus D_6 \bigoplus D_7 \bigoplus D_8\)
交叉奇偶校验:进行大量字节传送时,每字节横向校验,全部字节的同一位纵向校验,横校验无法检出的错误大概率会被纵校验检测出,从而降低错判概率。
2.汉明校验码
Richard Hamming于1950年提出,目前广泛采用的一种有效的校验码。主存的ECC(Error Correcting Code,错误检查与纠正)就是采用类似的技术。实质上是多重奇偶校验。
实现原理:在有效信息位中加入几个校验位,均匀拉大码距,将某一位的错误映射到几个校验位上,从而指出错误位置,便于自动纠错。校验位数K和信息位数N的关系为: \(2^{K-1}\geq N+K+1\) 例:对一个字节(8位)的数据进行汉明码编码。
步骤:
1.首先根据公式得出此时K=5,即总位数为13。记最高位位号为13,最低位为1(左高右低)。对于每个汉明码i(编号1~5),分配的位号为2^(i-1),若超过最高位号,则分配为最高位,其余为信息位。 \(P为校验位,D为信息位,则海明码可以表示为P_5D_8D_7D_6D_5P_4D_4D_3D_2P_3D_1P_2P_1\)
\[对应的编号为H_{13}H_{12}H_{11}H_{10}H_{9}H_{8}H_{7}H_{6}H_{5}H_{4}H_{3}H_{2}H_{1}\]2.为方便描述,对单个校验码采用偶校验,被检验的每一位位号等于校验它的各校验位的位号之和,即汉明码的位号实质上是参与校验的各校验位权值之和。 \(如:第一个信息位D_1,对应H_3,3即1+2,也就是说,D_1位对应的校验位为P_1和P_2;\)
\[第七个信息位D_7,对应H_{11},11即8+2+1,对应校验位为P_8、P_2和P_1。\]由此可以得出以下校验位的组成: \(P_1=D_1 \bigoplus D_2 \bigoplus D_4 \bigoplus D_5 \bigoplus D_7\)
\[P_2=D_1 \bigoplus D_3 \bigoplus D_4 \bigoplus D_6 \bigoplus D_7\] \[P_3=D_2 \bigoplus D_3 \bigoplus D_4 \bigoplus D_8\] \[P_4=D_5 \bigoplus D_6 \bigoplus D_7 \bigoplus D_8\]补充第五个校验位使得每一个数据项都在校验位中出现相同次数: \(P_5=D_1 \bigoplus D_2 \bigoplus D_3 \bigoplus D_5 \bigoplus D_6 \bigoplus D_8\) 现在,每个信息位在校验位中都出现了3次,即每个信息位发生变化时,必有3个校验位发生变化,即码距为4。
3.循环冗余校验码
1.编码方法
Cyclic Redundancy Check(CRC),在计算机网络、同步通信和磁表面存储器中广泛使用的一种校验码。
实现方法:通过除法建立信息位和校验位之间的关系,有效信息用多项式M(X)表示,将M(X)左移若干位,校验式为G(X),M(X)除以G(X),得到的余数多项式R(X)就是校验式。有效信息和校验位拼接构成CRC码。
编码方法:左为信息位,右为校验位,若信息位数为N,校验位数为K,则该码称为(N+K,N)码。

步骤:
1.把待编码的N位有效信息表示为多项式M(X)。
2.把M(X)左移K位,得到M(X)*X^K,空出的K位留给K位余数。
3.选取一个K+1位的多项式G(X),对M(X)*X^K做除(mod 2)。 \({M(X)\times X^K\over G(X)}=Q(X)+{R(X)\over G(X)}\) 4.把左移K位以后的有效信息与余数R(X)作加减(mod 2),拼接为共N+K位的CRC码。
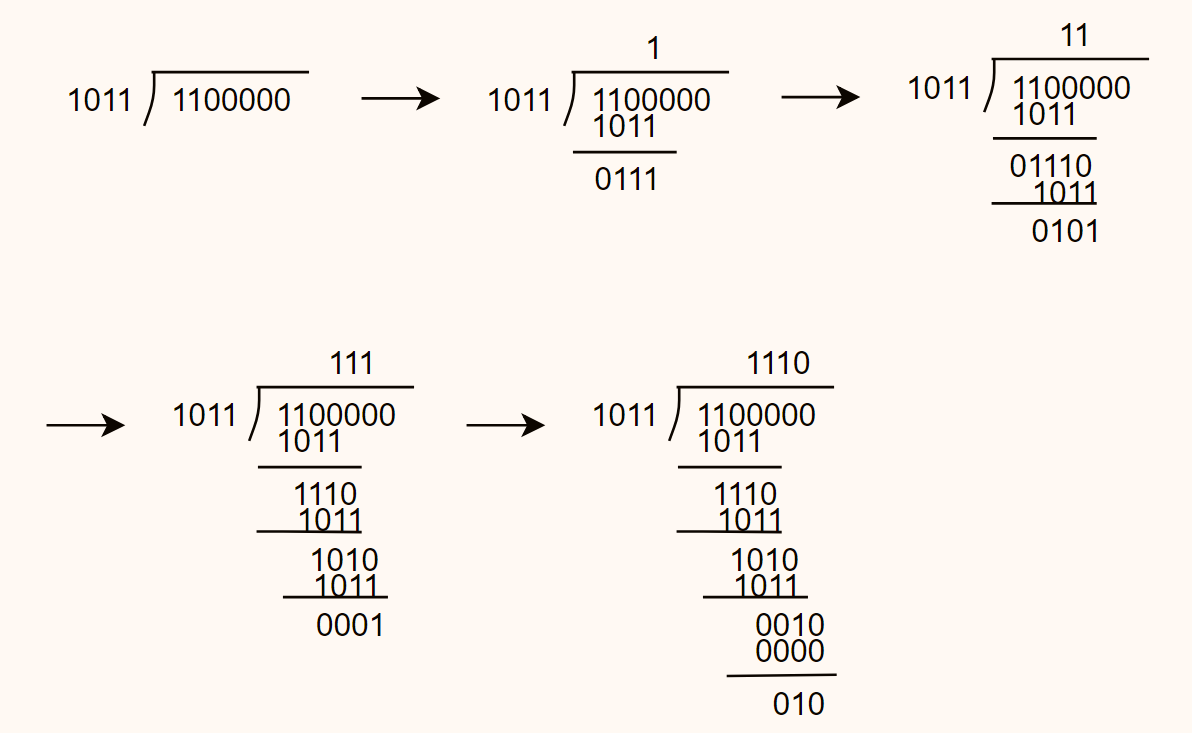
例:选择产生多项式G(X)=1011,把4位有效信息1100编成CRC码。 \(M(X)=X^3+X^2=1100\)
\[M(X)\times X^3=X^6+X^5=110,0000(即左移3位)\] \[G(X)=X^3+X+1=1011\] \[{M(X)\times X^3\over G(X)}={110,0000\over 1011}={010\over 1011}(模2下除法)\] \[M(X)\times X^3+R(X)=110,0000+010=110,0010\]得到所求的CRC码为1100010,这是一个(7,4)码。
模2运算是一种二进制算法,不考虑进位借位。模2加减法等同于按位异或;模2乘法类似与普通乘法,但在处理累加进位结果时采用模2加法法则;模2除法确定商时采用模2减法法则,不带借位,余数通过异或得到,若余数全0则商0,否则商1。
2.校验与纠错
CRC码被接收后,再次用G(X)去除,得到的余数为0则说明代码正确,否则表明某一位出错,然后由余数值确定出错位置。
| 码值 | 余数 | 出错位 |
|---|---|---|
| 1100010(正确码) | 000 | 无 |
| 1100011 | 001 | 7 |
| 1100000 | 010 | 6 |
| 1100110 | 100 | 5 |
| 1101010 | 011 | 4 |
| 1110010 | 110 | 3 |
| 1000010 | 111 | 2 |
| 0100010 | 101 | 1 |
假设出错,那么余数不为零,查表可得余数对应的出错位。对余数补0后继续进行除法,可得到下一个余数。(如:当余数为011,即出错位为4时,余数补0后为0110,用1011继续进行模2除法,可得余数110)继续进行除法直到把出错位移至最高位(在(7,4)码中对应第七位,最右边为第0位),然后通过异或门将最高位取反纠正。(出错位为x,对应做x次补0除法即可把出错位左移至最高位)
3.生成多项式G(X)的选择标准
(1)任意错误计算的余数均不能为0。
(2)不同位的错误对应不同的余数。
(3)对余数作模2除法应使余数循环。